Happy new year!
Group theory warm-up exercise for the year: what are all the groups of order 2024?
Last year we did 2023, which was rather boring because all groups of order 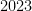 are abelian. This year the possibilities are much more numerous and the calculation is somewhat involved.
are abelian. This year the possibilities are much more numerous and the calculation is somewhat involved.
There are some easy initial reductions using Sylow’s theorem. Let  be a group of order
be a group of order  . Sylow’s theorem implies that there must be a unique subgroup
. Sylow’s theorem implies that there must be a unique subgroup 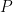 of order
of order 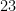 . Similarly, in the quotient
. Similarly, in the quotient 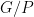 of order
of order 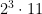 there must be a unique subgroup of order
there must be a unique subgroup of order 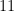 . Therefore
. Therefore  has a unique subgroup
has a unique subgroup  of order
of order  . Let
. Let 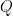 be a Sylow
be a Sylow  -subgroup of
-subgroup of  . Then
. Then  for some homomorphism
for some homomorphism  .
.
We can easily list the possibilities for  and
and 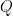 . There are just two possibilities for
. There are just two possibilities for  : the cyclic group
: the cyclic group 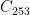 and the unique nonabelian semidirect product
and the unique nonabelian semidirect product  . There are five possibilities for
. There are five possibilities for 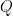 :
: 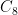 ,
, 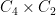 ,
,  , the dihedral group
, the dihedral group 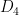 , and the quaternion group
, and the quaternion group  .
.
Next, for each choice of  and
and 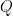 , we must consider all possibilities for
, we must consider all possibilities for  . However, in order to avoid duplication, we must determine when two homomorphisms
. However, in order to avoid duplication, we must determine when two homomorphisms  induce isomorphic semidirect products.
induce isomorphic semidirect products.
A quick word about notation. Following standard practice in group theory, we denote group actions on the right. If  and
and 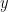 are elements of a common group
are elements of a common group  , we denote by
, we denote by  the conjugate
the conjugate  . We also denote by
. We also denote by 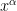 the image of
the image of  under a given homomorphism
under a given homomorphism 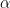 . We can then say that the semidirect product
. We can then say that the semidirect product  is generated by copies of
is generated by copies of  and
and 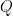 subject to the natural-looking relation
subject to the natural-looking relation
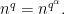
This relation asserts that the conjugation action of 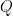 on
on  is given by
is given by 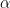 .
.
Suppose  is an isomorphism from
is an isomorphism from  to
to  such that
such that 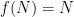 . Then
. Then  induces an automorphism
induces an automorphism 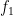 of
of  as well as an automorphism
as well as an automorphism  of
of  . These automorphisms are not arbitrary: they satisfy a certain compatibility relation. Namely, for all
. These automorphisms are not arbitrary: they satisfy a certain compatibility relation. Namely, for all 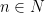 and
and 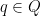 we have
we have
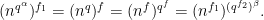
In other words, for all 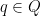 we have, in
we have, in 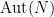 ,
,

Written a third way, we have, as elements of 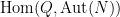 ,
,

where  denotes the inner automorphism of
denotes the inner automorphism of 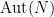 induced by
induced by 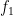 . (Alternatively, if somewhat more traditionally we denote function composition in a right-to-left manner, the compatibility relation is
. (Alternatively, if somewhat more traditionally we denote function composition in a right-to-left manner, the compatibility relation is  .)
.)
Let us denote by  the set of all isomorphisms
the set of all isomorphisms  such that
such that 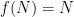 , and by
, and by 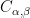 the set of all compatible isomorphism pairs
the set of all compatible isomorphism pairs  , i.e.,
, i.e.,

The import of the previous paragraph is that there is a natural map 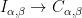 . Moreover this map is surjective (though typically not injective), because if
. Moreover this map is surjective (though typically not injective), because if  is a compatible isomorphism pair then the map
is a compatible isomorphism pair then the map 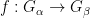 defined by
defined by 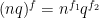 is an isomorphism (easy exercise). In particular, there is an isomorphism
is an isomorphism (easy exercise). In particular, there is an isomorphism  from
from  to
to 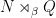 such that
such that 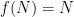 if and only if
if and only if 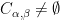 , i.e., if and only if there is a pair of compatible automorphisms
, i.e., if and only if there is a pair of compatible automorphisms  .
.
We can phrase this conclusion another way. Observe that  acts naturally on
acts naturally on 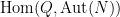 . The
. The 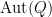 factor acts by precomposition, while the
factor acts by precomposition, while the 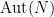 factor acts by conjugation. Isomorphism classes of split extensions
factor acts by conjugation. Isomorphism classes of split extensions 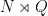 are in bijection with orbits of
are in bijection with orbits of  in
in 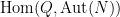 . (Here we consider
. (Here we consider  and
and 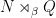 to be isomorphic as extensions if and only if there is an isomorphism
to be isomorphic as extensions if and only if there is an isomorphism  such that
such that 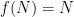 . In general this is more restrictive than mere isomorphism as groups.)
. In general this is more restrictive than mere isomorphism as groups.)
Now consider the special case in which 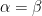 . In this case
. In this case  is a subgroup of
is a subgroup of  and
and  is a subgroup of
is a subgroup of  , and the natural map
, and the natural map 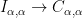 is a homomorphism. Let
is a homomorphism. Let 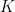 be the kernel. Then
be the kernel. Then 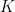 consists of all isomorphism
consists of all isomorphism 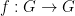 that restrict to the identity on
that restrict to the identity on  and induce the identity on
and induce the identity on  . This implies that there is a map
. This implies that there is a map 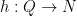 such that
such that 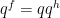 for all
for all 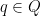 . Since
. Since  restricts to the identity on
restricts to the identity on  , we have
, we have
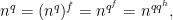
which implies that 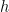 takes values in the centre
takes values in the centre  of
of  . Moreover,
. Moreover, 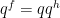 is a homomorphism
is a homomorphism  , so we must have the relation
, so we must have the relation

This relation means that 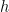 is a crossed homomorphism from
is a crossed homomorphism from 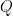 to
to  . The group of crossed homomorphisms
. The group of crossed homomorphisms  is usually denoted
is usually denoted  . Thus we have a short exact sequence
. Thus we have a short exact sequence
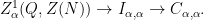
In particular, if  is a characteristic subgroup of
is a characteristic subgroup of  ,
,  is the full automorphism group, so we have a short exact sequence
is the full automorphism group, so we have a short exact sequence

In fact  can be identified with the subgroup of automorphisms of
can be identified with the subgroup of automorphisms of  preserving
preserving 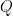 , so this sequence splits and we find that
, so this sequence splits and we find that

Let us put all this into practice. Recall that we have two possibilities for  :
: 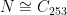 or
or 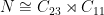 . Let us consider the case
. Let us consider the case 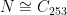 first. We have
first. We have
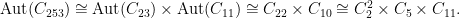
For each choice of 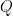 among
among 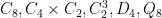 we must tabulate the homomorphisms
we must tabulate the homomorphisms  up to the action of
up to the action of 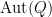 by precomposition and the conjugation action of
by precomposition and the conjugation action of 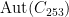 . Since
. Since 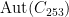 is abelian, the latter action is trivial. Any such homomorphism must take values in the Sylow
is abelian, the latter action is trivial. Any such homomorphism must take values in the Sylow  -subgroup
-subgroup 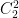 , so we are reduced to tabulating homomorphisms
, so we are reduced to tabulating homomorphisms  up to automorphisms of
up to automorphisms of 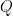 .
.
Case 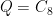 : There are four. Among these are groups with the structures
: There are four. Among these are groups with the structures 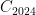 ,
,  ,
,  . The last has the structure
. The last has the structure 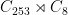 , and the action of
, and the action of 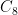 on
on 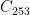 is fixed-point-free.
is fixed-point-free.
Case  : Write
: Write ![{Q = \langle x, y \mid x^4 = y^2 = [x,y] = 1\rangle}](https://s0.wp.com/latex.php?latex=%7BQ+%3D+%5Clangle+x%2C+y+%5Cmid+x%5E4+%3D+y%5E2+%3D+%5Bx%2Cy%5D+%3D+1%5Crangle%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Any homomorphism
. Any homomorphism  must kill
must kill 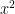 , so factors through
, so factors through ![{Q / \langle x^2 \rangle \cong \langle x, y \mid x^2 = y^2 = [x,y] = 1\rangle \cong C_2^2}](https://s0.wp.com/latex.php?latex=%7BQ+%2F+%5Clangle+x%5E2+%5Crangle+%5Ccong+%5Clangle+x%2C+y+%5Cmid+x%5E2+%3D+y%5E2+%3D+%5Bx%2Cy%5D+%3D+1%5Crangle+%5Ccong+C_2%5E2%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Naively are
. Naively are 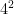 homomorphisms
homomorphisms  , but
, but 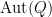 acts by swapping
acts by swapping  and
and 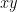 (while
(while 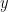 is fixed) and the number of orbits of homomorphisms
is fixed) and the number of orbits of homomorphisms  is
is  . These groups include
. These groups include 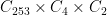 ,
, 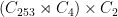 ,
, 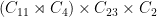 ,
,  ,
,  ,
, 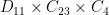 ,
,  , and
, and 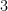 others.
others.
Case 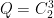 : There are
: There are  homomorphisms
homomorphisms  , but only
, but only 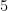 up to the action of
up to the action of  . They are in bijection with subgroups of
. They are in bijection with subgroups of 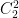 . The corresponding groups of order
. The corresponding groups of order  are
are 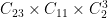 ,
,  ,
, 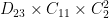 ,
, 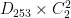 , and
, and  .
.
Case 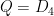 : Any homomorphism
: Any homomorphism 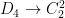 factors through
factors through 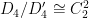 . Just as in the case of
. Just as in the case of 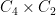 there are
there are 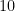 homomorphisms
homomorphisms 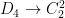 up to the action of
up to the action of  . The groups of order
. The groups of order  include
include 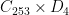 and
and 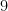 in which
in which 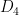 acts nontrivially on
acts nontrivially on 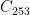 by conjugation.
by conjugation.
Case  : Any homomorphism
: Any homomorphism 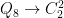 factors through
factors through  . In this case
. In this case 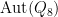 acts on
acts on 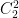 as
as  , so as in the case of
, so as in the case of  there are just
there are just 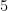 homomorphisms
homomorphisms 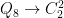 up to automorphisms of
up to automorphisms of  . Thus there are
. Thus there are 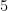 semidirect products of the form
semidirect products of the form  .
.
Now consider the case in which 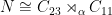 is nonabelian. Since
is nonabelian. Since 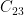 is a characteristic subgroup of
is a characteristic subgroup of  (being the only subgroup of order
(being the only subgroup of order 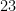 ), we have
), we have

where  is the subgroup of
is the subgroup of 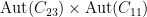 consisting of compatible pairs. Consider the compatibility relation
consisting of compatible pairs. Consider the compatibility relation 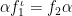 . Since
. Since  is abelian,
is abelian,  is trivial, so the relation reduces to
is trivial, so the relation reduces to  . Since
. Since 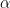 is injective, this implies that
is injective, this implies that  is trivial. Therefore
is trivial. Therefore  . Meanwhile one checks that
. Meanwhile one checks that  . Therefore
. Therefore  . Now if
. Now if 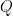 has order
has order 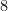 then any homomorphism
then any homomorphism  takes values in a Sylow
takes values in a Sylow  -subgroup isomorphic to
-subgroup isomorphic to 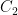 , which are all conjugate. Tabulating homomorphisms
, which are all conjugate. Tabulating homomorphisms 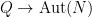 up to the natural action of
up to the natural action of  is therefore equivalent to tabulating homomorphisms
is therefore equivalent to tabulating homomorphisms  up to automorphisms of
up to automorphisms of 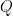 , which just amounts to tabulating automorphism classes of subgroups of
, which just amounts to tabulating automorphism classes of subgroups of 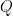 of index at most
of index at most  . This case is therefore somewhat easier than the previous one.
. This case is therefore somewhat easier than the previous one.
Case 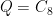 : There are just two. The corresponding groups of order
: There are just two. The corresponding groups of order  have the forms
have the forms  and
and 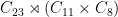 .
.
Case  : There are three, corresponding to subgroups isomorphic to
: There are three, corresponding to subgroups isomorphic to 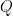 ,
,  , and
, and 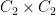 . The corresponding groups of order
. The corresponding groups of order  include
include  ,
,  ,
,  .
.
Case 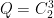 : There are two, since all index-
: There are two, since all index- subgroups are essentially the same. The corresponding groups of order
subgroups are essentially the same. The corresponding groups of order  are
are 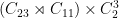 and
and  .
.
Case 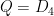 : There are three, since there is a unique subgroup isomorphic to
: There are three, since there is a unique subgroup isomorphic to  while the two subgroups isomorphic to
while the two subgroups isomorphic to 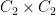 are equivalent by an automorphism. There are three corresponding groups with structure
are equivalent by an automorphism. There are three corresponding groups with structure  .
.
Case  : There are two, since the three subgroups of
: There are two, since the three subgroups of  isomorphic to
isomorphic to  are equivalent by automorphisms. Thus there are just two groups with the structure
are equivalent by automorphisms. Thus there are just two groups with the structure  .
.
Thus altogether there are 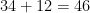 groups of order
groups of order  .
.