I mentioned before the following theorem of Hofmann and Russo, extending earlier work by Levai and Pyber on the profinite case.
Theorem 1 (Hofmann and Russo) If
is a compact group of positive commuting probability then the FC-center
is an open subgroup of
with finite-index center
.
(I actually stated this theorem incorrectly previously, asserting the conclusion as well; this is clearly false in general, for instance for
.)
Here the FC-center of a group is the subgroup of elements with finitely many conjugates. In general a group is called FC if each of its elements has finitely many conjugates, and BFC if its elements have boundedly many conjugates. A theorem of Bernhard Neumann states that a group is BFC if and only if
is finite.
I noticed today that one can prove this theorem rather easily by adapting the proof of Peter Neumann’s theorem that a finite group with commuting probability bounded away from is small-by-abelian-by-small. Some parts of the argument below are present in scattered places in the above two papers, but I repeat them for completeness.
Proof: Let be the normalised Haar measure of
, and suppose that
Let be the set of elements in
with at most
conjugates. Then
is closed, since any element
with at least
distinct conjugates
has a neighbourhood
such that for all
the points
are distinct. Since
we see that for all
. This implies that the group
generated by
is generated in at most
steps, i.e.,
, which implies that
is an open BFC subgroup of
. Since
is an increasing sequence of finite-index subgroups it must terminate with some subgroup
, and in fact
must be the FC-center of
. This proves that
is an open BFC subgroup of
.
In particular in its own right is a compact group with
finite (by the theorem of Bernhard Neumann mentioned at the top of the page). Since the commutator map
is a continuous map to a discrete set satisfying
there must be a neighbourhood
of
such that
. This implies that
is open, hence of finite-index in
.
For me, the Hofmann-Russo theorem is a negative result: it states that commuting probability does not extend in an interesting way to the category of compact groups. To be more specific we have the following corollary.
Corollary 2 If
is a compact group of commuting probability
then there is a finite group
also of commuting probability
.
We need a simple lemma before proving the corollary.
Lemma 3 For each
there is a finite group
of commuting probability
.
Proof: If is odd then
has commuting probability
. We can use this formula alone and induction on
to define appropriate groups
. Take
and
. If
is even take
. If
take
. If
take
.
An isoclinism between two groups and
is a pair of isomorphisms
and
which together respect the commutator map
. Clearly isoclinism preserves commuting probability. A basic theorem on isoclinism, due to Hall, is that every group
is isoclinic to a stem group, a group
satisfying
. We can now prove the corollary.
Proof: Proof of corollary: By the theorem the FC-center of
has finite-index, say
, and moreover
has finite-index center
and therefore finite commutator subgroup
. Let
be a stem group isoclinic to
. Then
and
have the same commuting probability, and
is finite since
,
, and
, so we can take
.
Beautiful proof! One point, which is not clear to me:”This implies that the group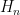 generated by
generated by  is generated in at most
is generated in at most  steps” – why?
steps” – why?
LikeLike
Hi, thanks for your comment! This is a useful lemma. Suppose is a symmetric subset of a group
is a symmetric subset of a group  containing the identity, and suppose
containing the identity, and suppose 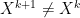 . Pick
. Pick  . Then
. Then 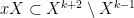 . Thus if
. Thus if  has a Haar measure
has a Haar measure 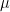 then
then 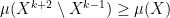 whenever
whenever 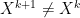 . Thus if
. Thus if  then
then 
LikeLike
Hello and thank you for your prompt and clear reply! Indeed, a very nice and useful Lemma.Actually, after carefully working-out all the steps of the proof, I realized that there are two other points there, which I wanted to understand. Could you, please, help me with them?First one: Since is a subset of
is a subset of  , it follows that
, it follows that  is equal to some
is equal to some  for some large-enough
for some large-enough  . This is actually explicitly stated in your proof, when you say that
. This is actually explicitly stated in your proof, when you say that  , which is FC-center, is also BFC-subgroup. But that implies that
, which is FC-center, is also BFC-subgroup. But that implies that  is also closed (again, this is stated explicitly in the proof, when you say that
is also closed (again, this is stated explicitly in the proof, when you say that  is compact). Thus,
is compact). Thus,  is the connected component of the identity in
is the connected component of the identity in  (which is a normal subgroup of
(which is a normal subgroup of  ). Thus, the index
). Thus, the index 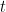 of
of  in
in  is just the number of connected components of
is just the number of connected components of  . Moreover, the multiplication in
. Moreover, the multiplication in  defines a binary operation on the set of connected components of
defines a binary operation on the set of connected components of  , making it a finite group
, making it a finite group 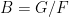 . Am I right? Second one: why is
. Am I right? Second one: why is ![[F,F]](https://s0.wp.com/latex.php?latex=%5BF%2CF%5D&bg=ffffff&fg=000000&s=0&c=20201002) finite? How does it follow from the facts, that
finite? How does it follow from the facts, that  is a BFC-group and that
is a BFC-group and that  is compact?
is compact?
LikeLike
Again, thank you so much for your time and help!
LikeLike
Being an open subgroup (and therefore in particular a closed subgroup), contains the connected component of the identity, but
contains the connected component of the identity, but  itself need not be connected. The connected component of the identity might even be trivial.That being said, yes
itself need not be connected. The connected component of the identity might even be trivial.That being said, yes  is an open normal subgroup and so
is an open normal subgroup and so  is a finite group. Also if
is a finite group. Also if  is the connected component of the identity in
is the connected component of the identity in  then
then  is a normal subgroup and so
is a normal subgroup and so  is a (not necessarily finite) group.The finiteness of
is a (not necessarily finite) group.The finiteness of ![[F,F]](https://s0.wp.com/latex.php?latex=%5BF%2CF%5D&bg=ffffff&fg=000000&s=0&c=20201002) is equivalent to the BFC-ness of
is equivalent to the BFC-ness of  . The left-to-right direction of this is easy: if
. The left-to-right direction of this is easy: if  then
then ![e^{-1} e^f \in [F,F]](https://s0.wp.com/latex.php?latex=e%5E%7B-1%7D+e%5Ef+%5Cin+%5BF%2CF%5D&bg=ffffff&fg=000000&s=0&c=20201002) , so
, so  has at most
has at most ![|[F,F]|](https://s0.wp.com/latex.php?latex=%7C%5BF%2CF%5D%7C&bg=ffffff&fg=000000&s=0&c=20201002) conjugates. The other direction is a theorem of Bernhard Neumann. In the compact case one can prove it as follows: Take a commutator
conjugates. The other direction is a theorem of Bernhard Neumann. In the compact case one can prove it as follows: Take a commutator ![c = [e,f]=e^{-1}f^{-1}ef](https://s0.wp.com/latex.php?latex=c+%3D+%5Be%2Cf%5D%3De%5E%7B-1%7Df%5E%7B-1%7Def&bg=ffffff&fg=000000&s=0&c=20201002) . If one replaces
. If one replaces  with any element
with any element  of
of 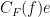 , and then
, and then  with any element
with any element  of
of 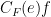 , then still
, then still ![[e,f]=c](https://s0.wp.com/latex.php?latex=%5Be%2Cf%5D%3Dc&bg=ffffff&fg=000000&s=0&c=20201002) . If
. If  is
is  -BFC then
-BFC then  and
and 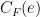 both have index at most
both have index at most  , so
, so ![\mu(\{(e,f)\in F^2 : [e,f]=c\}) \geq 1/n^2](https://s0.wp.com/latex.php?latex=%5Cmu%28%5C%7B%28e%2Cf%29%5Cin+F%5E2+%3A+%5Be%2Cf%5D%3Dc%5C%7D%29+%5Cgeq+1%2Fn%5E2&bg=ffffff&fg=000000&s=0&c=20201002) , so there are at most
, so there are at most 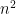 commutators
commutators  . Now the task is reduced to showing that if
. Now the task is reduced to showing that if  has finitely many commutators then
has finitely many commutators then ![[F,F]](https://s0.wp.com/latex.php?latex=%5BF%2CF%5D&bg=ffffff&fg=000000&s=0&c=20201002) is finite, which is a classical theorem of Schur.
is finite, which is a classical theorem of Schur.
LikeLike